Brüche, Brucharten, Bruchrechnung - Grundlagen & Übungen
Brüche darstellen und bestimmen / Brucharten / Bruchrechnung: Erklärung, Beispiele und Übungen für Mathe 5./6. Klasse.
Brüche
Ein Bruch steht für eine Division, wobei der Zähler durch den Nenner geteilt wird.
In einem Bruch zeigt der Nenner an, in wie viele Teile ein Ganzes geteilt wurde, und der Zähler gibt an, wie viele Stücke davon man hat.
Unechter Bruch - der Zähler ist größer als der Nenner.
Gemischte Zahl (gemischter Bruch) - besteht aus einer ganzen Zahl und einem Bruch.
Ein echter Bruch mit dem Zähler 1 und einem beliebigen Nenner ist ein Stammbruch - der kleinstmögliche Anteil eines bestimmten Bruchs.
Echter Bruch - der Nenner ist größer als der Zähler.
einen Bruch kürzen
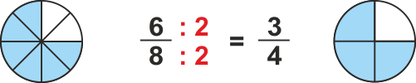
bedeutet den Zähler und Nenner durch die gleiche Zahl zu teilen
einen Bruch erweitern
bedeutet den Zähler und den Nenner mit der gleichen Zahl zu multiplizieren.
Der Wert des Bruchs ändert sich in beiden Fällen nicht, nur die Schreibweise.
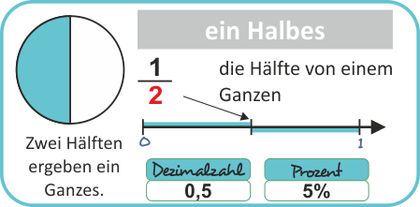
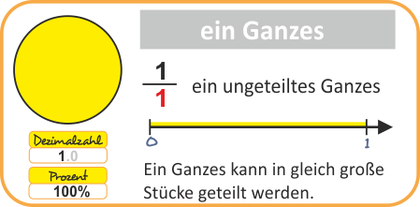
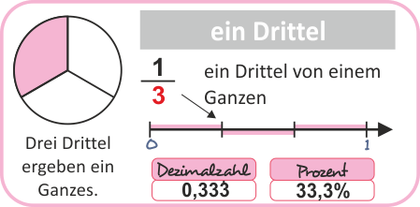
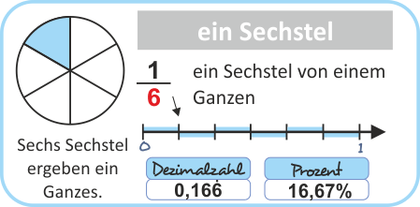
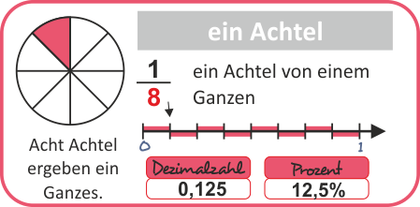
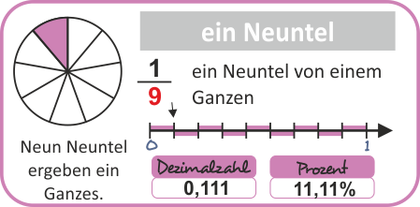
Übersicht und Erläuterungen - Mathe Lernposter - als PDF zum Ausdrucken
Sprache der Mathematik
Anstatt Arbeitsblätter einzeln ausdrucken zu müssen, gibt es hier eine Arbeitsblättersammlung zum Thema Brüche und Brüchrechnung
Erläuterungen und Übungen für Mathematik zum Thema Brüche und Bruchrechnung: Darstellen von Brüchen, Brüche kürzen und erweitern, Brucharten, Brüche am Zahlenstrahl, Brüche vergleichen, Brüche addieren und subtrahieren, Brüche multiplizieren, Brüche dividieren mit Kehrwert, Bruchteile von Ganzen - Bruchteil, Anteil und Ganzes, Prozentzahl als Darstellung einer BruchzahlDie Arbeitsblättersammlung finden Sie hier:
- 58 Seiten mit verschiedenen Aufgaben und Übungen als PDF zum Herunterladen und Ausdrucken
- Lösungen zu den Aufgaben
