Rechenregeln mit ganzen Zahlen
Rechenregeln mit ganzen Zahlen: Erklärung, Beispiele und Übungen für Mathe 5./6. Klasse.
Interaktive Übungen
Klicke auf den Link, dann kommst du sofort zur interaktiven Übung. (Hier ist ein Beispiel mit Anleitung)
Rechenregeln mit ganzen Zahlen
Klammerregeln
KlaPoPuStri Regel - Eine Klammer wird zuerst berechnet, dann Potenzen dann Punktrechnungen und zuletzt Strichrechnungen. Sonst wird von links nach rechts gerechnet! Auch innerhalb der Klammern gilt: Potenzen vor Punktrechnung vor Strichrechnung und von links nach rechts rechnen!
Beispiel:
Klammerarten - Es gibt drei Arten von Klammern: runde Klammern: ( ) ; eckige Klammern: [ ] ; geschweifte Klammern: { }
Die runde Klammer wird am häufigsten verwendet. Die anderen beiden Klammerarten werden verwendet, wenn eine Rechnung komplizierter ist und eine Klammer innerhalb einer anderen Klammer vorkommt. Hierbei gilt: eckige Klammern kommen um runde Klammern und geschweifte Klammern kommen um
eckige Klammern.
Bei mehreren Klammern rechnet man von innen nach außen. Man beginnt also mit den runden Klammern ( ), dann werden die eckigen Klammern [ ] und abschließend die geschwungenen Klammern { } aufgelöst (in der Reihenfolge rund – eckig – geschweift).
Klammerregel - Plusklammer
Steht ein Pluszeichen (+) vor der Klammer, in der eine Summe oder eine Differenz steht, kann man die Klammern einfach weglassen.
+ (a+b+c) = a + b + c
Beispiel:
4 + (11 - 3 + 5) = 4 + 11 - 3 + 5
Klammerregel - Minusklammer
Steht ein Minuszeichen (-) vor der Klammer, in der eine Summe oder eine Differenz steht, muss man alle Vorzeichen der Termglieder innerhalb der Klammer umdrehen, bevor man die Klammer weglässt.
- (a+b-c) = -a - b + c
Beispiel:
4 - (11 - 3 + 5) = 4 - 11 + 3 - 5
9 - (-15 + 4 - 9) = 9 + 15 - 4 + 9
Kommutativgesetz der Addition („Vertauschungsgesetz“)
Es ist egal, in welcher Reihenfolge die Zahlen bei einer Addition stehen.
a + b = b + a
Beispiel:
(-4) + 3 = 3 + (-4)
(-2) + (-6) = (-6) + (-2)
Kommutativgesetz der Multiplikation („Vertauschungsgesetz“)
Es ist egal, in welcher Reihenfolge die Zahlen bei einer Multiplikation stehen.
a · b = b · a
Beispiel:
(-7) · 2 = 2 · (-7)
(-4) ·(-3) = (-3) · (-4)
Assoziativgesetz Addition („Verbindungsgesetz“)
Bei der Addition 3 oder mehr Zahlen können die Klammern beliebig gesetzt oder weggelassen werden.
a + b + c = (a + b) + c = a + (b + c)
Beispiel:
3 + (7 + 9) = (3 + 7) + 9
8 + (6 + (-5)) = (8 + 6) + (-5)
Assoziativgesetz Multiplikation („Verbindungsgesetz“)
Bei der Multiplikation von 3 oder mehr Zahlen können die Klammern beliebig gesetzt oder weggelassen werden.
a · b · c = (a · b) · c = a · (b · c)
Beispiel:
4 · (5 · 3) = (4 · 5) · 3
2 · ((-3) · 10) = (2 · (-3)) · 10
Achtung! Weder Kommutativgesetz noch Assoziativgesetz gelten für Subtraktion, Division oder eine Mischung von Rechenarten.
Distributivgesetz („Verteilungsgesetz“)
Wenn eine Summe oder Differenz mit einer Zahl multipliziert wird, kannst du ausmultiplizieren - jede Zahl in der Klammer wird einzeln mit dem Faktor multipliziert und die Produkte werden addiert oder subtrahiert. Es geht auch umgekehrt: Wenn die Glieder einer Summe oder Differenz den gleichen Faktor haben, kannst du ausklammern - diese Summe oder Differenz in ein Produkt umwandeln.
Ausmultiplizieren
Beispiel:
(-4 + 9) · 5 = -4 · 5 + 9 · 5
Ausklammern
Beispiel:
-4 · 5 + 9 · 5 = (-4 + 9) · 5
Ausmultiplizieren
Beispiel:
(9 - 3) · 6 = 9 · 6 - 3 · 6
Ausklammern
Beispiel:
9 · 6 - 3 · 6 = (9 - 3) · 6
Wir können das Distributivgesetz nutzen, um damit vorteilhaft zu rechnen. In den Klammern können beliebig viele Summanden stehen.
Das Distributivgesetz gilt auch für die Division: Dividiert man eine Summe durch eine Zahl oder dividiert man die einzelnen Summanden durch diese Zahl, ändert sich das Ergebnis nicht. Dabei muss die Zahl, durch die geteilt wird, rechts von der Klammer stehen.
(a + b) : c = a : c + b : c
(-72 + 18) : 9
= -72 : 9 + 18 : 9
= -8 + 2
= -6
(a - b) : c = a : c - b : c
(-100 - 35) : 5
= -100 : 5 - 35 : 5
= -20 - 7
= -27
Achtung! Wenn die Klammer rechts vom „:“ steht, gilt das Distributivgesetz nicht! c : (a+b)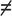 
c : a + c : b
c : a + c : bErklärung, Regeln & Übungen / Arbeitsblätter mit Lösungen
- als PDF zum Ausdrucken
