Quadratzahlen

Quadratzahlen & Quadrieren: Erklärung, Beispiele und Übungen
Interaktive Übungen
Klicke auf den Link, dann kommst du sofort zur interaktiven Übung. (Hier ist ein Beispiel mit Anleitung)
Quadratzahlen
Multipliziert man eine natürliche Zahl mit sich selbst erhält man eine Quadratzahl. Die Rechenoperation heißt Quadrieren.

Wir sagen „a hoch zwei“, „a zum Quadrat“ oder kurz „a Quadrat“.
Quadratzahlen sind also Potenzen mit dem Exponenten 2 und einer natürlichen Zahl als Basis.

„acht hoch zwei“ oder „acht Quadrat ergibt 64" oder „64 ist acht zum Quadrat“
Quadratzahlen des kleinen Einmaleins
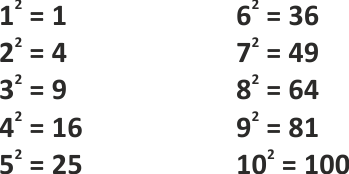
Merke:
- Das Quadrat jeder natürlichen Zahl ist eine natürliche Zahl.
- Das Quadrat von 0 ist 0.
- Das Quadrat jeder Zahl ungleich 0 ist immer positiv.
Multipliziert man zwei negative Zahlen miteinander, so ist das Ergebnis positiv.
Quadrieren von Dezimalzahlen
Die Quadrate der natürlichen Zahlen nennt man Quadratzahlen, es können aber auch Quadrate von beliebigen ganzen oder rationalen Zahlen gebildet werden.
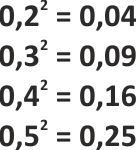
Schau genau: Die Anzahl der Nachkommastellen in der Grundzahl verdoppelt sich, wenn man sie quadriert. Man kann also die Nullen der Zahl weglassen und die Zahl ohne Nullen Quadrieren. Danach verdoppelt man die Anzahl der Nachkommastellen und schreibt das Komma sowie die notwendigen Nullen entsprechend auf.
Beispiel:

Tipp: Man kann die Zahlen, die keine Quadratzahlen sind, ganz einfach erkennen. Es gibt keine Quadratzahl, die auf 2, 3, 7 oder 8 endet. Die letzte Stelle einer Quadratzahl ist immer eine 1, 4, 5, 6, 9 (aber nicht alle Zahlen, die mit 1, 4, 5, 6 und 9 enden, sind Quadratzahlen!).
Damit kann man in vielen Fällen schnell ausschließen, dass eine Zahl eine Quadratzahl ist.
Quadrieren von Quotienten
Dividiert man die Quadrate zweier Zahlen, so erhält man das gleiche Ergebnis wie beim Quadrieren des Quotienten der beiden Zahlen.
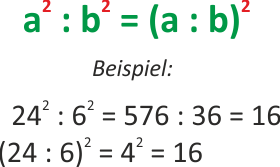
Quadrieren von Produkten
Multipliziert man die Quadrate zweier Zahlen, so erhält man das gleiche Ergebnis wie beim Quadrieren des Produktes der beiden Zahlen.

Quadrieren von Summen und Differenzen:


Diese Formeln bieten auch Hilfe beim Kopfrechnen. Das Quadrat einer beliebigen natürlichen Zahl zwischen 10 und 100 lässt sich einfach mit der binomischen Formel bestimmen, indem man die Zahl als Summe/Differenz einfacherer Zahlen (Vielfache von 10 oder einstellige Zahlen) darstellt.
Beispiel:

Erklärung, Regeln & Übungen / Arbeitsblätter mit Lösungen
- als PDF zum Ausdrucken





